Início > MTM5160 - Matemática Comercial e Financeira > Porcentagem, potências, raízes, Progressões Geométricas (PGs), Shifting e Dízimas Periódicas
28 de agosto de 2024 por LUIZBRUG
Índice:
- Resolução do exercício 7 do capítulo 1 (feito em sala de aula)
- Exercício (g) da 1) do Capítulo 1
- Técnica de Shifting (deslocamento)
- Outro exemplo de uso do Shifting
- Shifting com Dízima Periódica
- Shifting com Dízima Periódica 2
- Notas
Resolução do exercício 7 do capítulo 1 (feito em sala de aula):
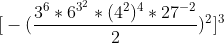
1) Se o expoente é ímpar, o resultado é negativo:
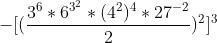
2) Multiplique o expoente dos parênteses ^2 com o expoente dos colchetes ^3, resultando em ^6. Somem os colchetes e sobram apenas os parênteses:
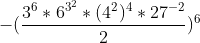
3) Transforme tudo em números primos:
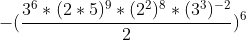
4) Multiplique os expoentes de dentro e fora dos parênteses:
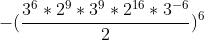
5) Continue simplificando ao somar os expoentes dos respectivos números primos. Lembre-se que a soma de 2^9 + 2^16 resultará em 2^25, porém o número é fracionado por 2, resultando em 2^24 (perde,portanto, 1 de expoente):
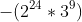
6) Finalmente, simplificamos para -2^144 * 3^54:
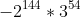
Exercício (g) da 1) do Capítulo 1:
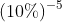
1) Transforma 10% em fração:
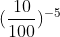
2) Divida 10 por 100 e remova o número dos parênteses:
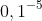
3) O expoente ^-5 ficará positivo se 0,1 se tornar fração de 1:
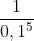
4) No caso de 0,1, se elevado a ^2 por exemplo, será 0,01 (dois 0s). Portanto, se elevado a ^5, serão cinco 0s, ou seja, 0,00001:
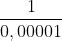
5) 1/0,00001 será igual a 10^5:
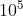
Técnica de Shifting (deslocamento)
A técnica Shifting pode ser usada com Progressões Geométricas (PGs).
Exemplo de Progressão Geométrica de termo inicial 3 e razão 2:
3, 6, 12, 24, 48, 96...
A Progressão Geométrica acima é de termo inicial 3 porque começa com o número 3 e é de razão 2 porque seus termos são sempre multiplicados por 2 (ex.: 3 * 2 = 6; 6 * 2 = 12; 12 * 2 = 24...)
1) Logo, como achamos a soma de uma Progressão Geométrica? Como achamos a soma de uma PG de termo inicial 3 com razão 2 até sua progressão em 96? Utilizamos a técnica Shifting (deslocamento), e ela segue um passo a passo. Primeiro multiplicamos a soma pela razão, ou seja, 3 * 2 = 6. Depois deslocamos o resultado à direita, como vemos abaixo respectivamente:
S = 3 + 6 + 12 + 24 + 48 + 96
S2 = 6 + 12 + 24 + 48 + 96 + 192
2) Designamos um sinal de menos ou mais para S ou S2. Um tem que ser menos e outro mais (-+). Logo, fazemos a soma:
(-) S = 3 + 6 + 12 + 24 + 48 + 96
(+) S2 = 6 + 12 + 24 + 48 + 96 + 192
-S somado com S2 dá S. -3 somado com 0 dá -3. -6 corta com 6, -12 corta com 12 e assim por diante. O único que sobra é 192. Logo:
S = -3 + 192 = 189
Outro exemplo de uso do Shifting
S = 2^3 + 2^4 + 2^5 + 2^6 + ... 2^10
2S = + 2^4 + 2^5 + 2^6 + ... 2^10 + 2^11
1) Atribui-se um sinal de positivo ou negativo para cada progressão e se faz a soma:
-S = 2^3 = 2^11
2) Multiplica-se por -1, faz-se os cálculos e obtém-se o resultado (em negrito):
S = -2^3 + 2^11 = -8 + 2048 = 2040
Shifting com Dízima Periódica
x = 0,16161616...
1) Logo:
(-) x = 0,16161616...
(+) 100x = 16,16161616...
2) Ficará 99x = 16. Se fizer na calculadora 16/99 = 0,16161616...
Shifting com Dízima Periódica 2
x = 8,579579579...
1) Fazemos então o Shifting:
(-) x = 8,579579579...
(+) 1000x = 8579,579579579...
2) Faz-se a soma e chegaremos em 999x = 8571. Logo, x = 8571/999 = 8,579579579...
Último exemplo de Shifting
x = 1/2 + 1/4 + 1/8 + 1/16 + ...
1) Essa é uma Progressão Geométrica (PG) de termo inicial 1/2 e razão 1/2 (se perceber, 1/2 * 1/2 = 1/4; 1/4 * 1/2 = 1/8; e assim por diante). Aplica-se Shifting (ou seja, multiplicar pela razão):
(+) x = 1/2 + 1/4 + 1/8 + 1/16 + ...
(-) 1/2x = 1/4 + 1/8 + 1/16 + ...
2) x - 1/2x = 1/2x. O resto é cortado e sobra 1/2. Logo, fica assim: 1/2x = 1/2. Chegando a isso, temos x = 1/2 dividido por 1/2, e esse valor fica 1. Resposta final é x = 1
Notas:
Livro da disciplina: GUERRA, Fernando. TANEJA, Inder Jeet. Matemática Financeira
- Link para download (UFSC)
- A ordem de acompanhamento e leitura do livro será: Cáp. 1, Cáp. 3 e Cáp. 2.
- Nessa última aula do dia 28, foi-se recomendado procurar exercícios com potências e raízes e treinar muito em casa.
- Recomendou-se também dar uma olhada nos trabalhos do Moodle (não necessariamente resolvê-los).
- Verificar também o Gabarito Comunitário do Moodle.
